Il y a des fonctions dont la limite est dite infinie. C'est-à-dire que si on trace la courbe de cette fonction, on se rend compte qu'elle se dirige infiniment vers sa limite, en s'en rapprochant chaque fois un peu plus, mais sans jamais l'atteindre.

 Par exemple, la fonction f(x) = x² a une limite infinie qui tend vers l'infini (on écrira « lim(x→∞) x² = ∞ », ce qui veut dire que quand x se rapproche de l'infini, bah x² aussi : mais x comme x² ne peuvent jamais atteindre l'infini), et la fonction g(x) = 1/x a une limite infinie qui tend vers 0 (on écrira « lim(x→∞) 1/x = 0 », ce qui veut dire que quand x se rapproche de l'infini, 1/x se rapproche de 0, mais n'atteint jamais 0).

 Pour ceux qui ont du mal à visualiser, voici un autre exemple : imaginez qu'on prenne le nombre 0,9 et qu'on rajoute un 9 à chaque fois. Ça nous fait donc 0,9 puis 0,99 puis 0,999 puis 0,9999, etc. A chaque fois le nombre grandit et se rapproche de 1, mais il n'atteint jamais 1 ! (Et si vous faites ça sur un graphique, vous verrez que vous aurez une courbe qui se penchera avant d'atteindre la barre du 1.) 

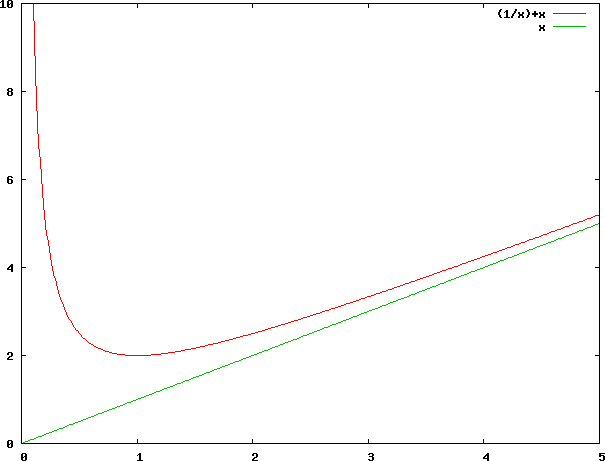
Juste une image d'asymptote prise au pif sur Google Image

 Quand une courbe se rapproche à l'infini d'une droite (ou même d'un point ou d'autre chose, mais on va prendre une droite parce que c'est plus joli et qu'en plus une droite c'est aussi une courbe) sans jamais l'atteindre, on parle d'asymptote, ce qui est un très joli mot. Asymptote, ça vient du grec ancien (du préfixe privatif ἀ- et du nom σύμπτωσις), et littéralement, ça veut dire sans rencontre (parce que les deux courbes ne se rencontrent jamais). L'asymptote, c'est quand une courbe tend infiniment vers une autre courbe sans jamais la toucher.

 L'asymptote, c'est quand une courbe est amoureuse d'une autre, en fait. C'est une belle histoire d'amour, silencieuse, sans heurt – et même sans histoire. Certains voient dans l'amour asymptote un amour-désir, et c'est sûrement vrai.  Peut-être aussi qu'il tient de l'amour impossible, et que c'est ce qui est si beau dans l'asymptote. Mais au-delà de ça, l'amour asymptote, c'est surtout un amour pur, entièrement pur, et infini – au sens propre du terme. Peut-on seulement imaginer la force qu'il faut pour tendre vers l'autre éternellement, infiniment, sans hésitations ni remous, toujours plus proche mais sans jamais l'atteindre ?

 Je trouve qu'on ne parle pas assez de cette histoire d'amour, qu'on ne parle pas assez de ces deux courbes qui ne se rejoindront jamais mais chemineront éternellement l'une à côté de l'autre l'une vers l'autre.

 (Cheminent déjà et ont déjà cheminé, puisque ce sont des courbes, leur existence est en dehors du temps, et leur éternité est déjà commencée et finie dans les mathématiques.)